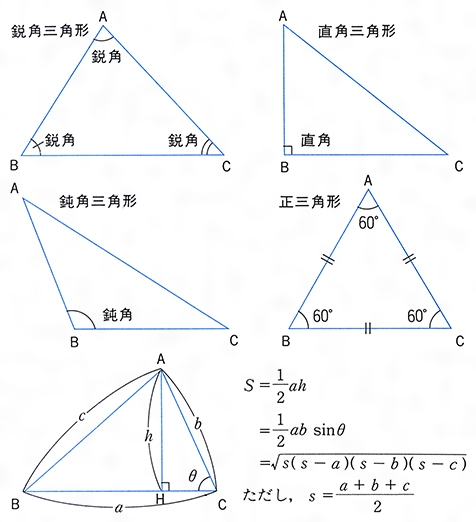
鋭角三角形 a b c abc a bc の各辺上を p, q, r p,q,r p, q, r が動く。 l = p q q r r p l=pqqrrp l = pq qr rp が最小になるのは, p q r pqr pqr が垂足三角形のとき。 線分和の最小値を考えるときは,折れ線にしましょう。 証明 p p p を a b ab a b に関して折り返した点を p 1 p_1 p 1 とし, a c ac a c に鋭角三角形の場合、内接中心Iと垂心Hの間の距離は I H r 2 , {\displaystyle IH を満たします。ここで、rは内接円半径であり、鈍角三角形の場合は逆の不等式です。 内接正方形 鋭角三角形の内接正方形の1つが辺の長さx a で、もう1つが辺の長さx b でx a x b 、次に 鋭角三角形 :すべての角が鋭角 (90°未満)である三角形 直角三角形 :1つの角が直角 (90°)である三角形 鈍角三角形 :1つの角が鈍角(90°より大きい)三角形
2
鋭角三角形とは
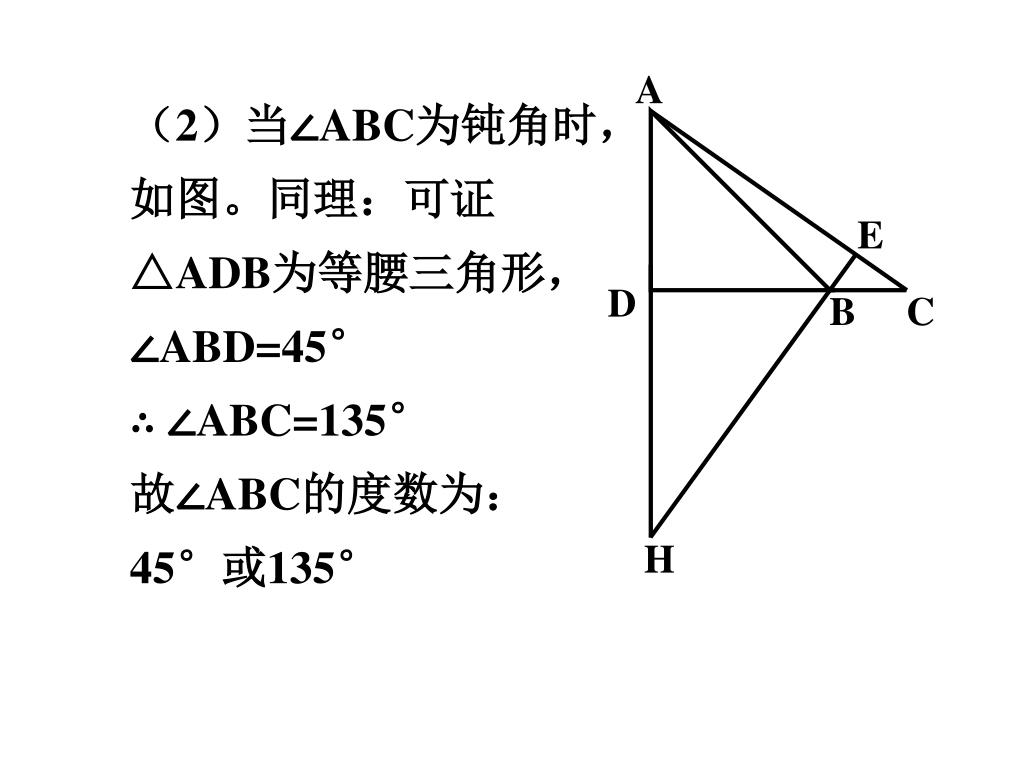
鋭角三角形とは-例文 鋭角三角形 という 三角形 例文帳に追加 a triangle called an acute angled triangle EDR日英対訳辞書 内角がすべて 鋭角 である 三角形 例文帳に追加 a triangle whose interior angles are all acute 日本語WordNet その係合部5aは、先端が 鋭角 な 三角形 状に設けられている 鋭角三角形の場合は、特に ∠A について示せば十分です。 上図のように、外接円の中心 O から辺 BC に下ろした垂線の足を H としましょう。 円周角の定理より ∠BOC = 2A となり、△BOH ≡ △COH ですので(※) ∠BOH = ∠COH = A および BH = CH = がしたがいます。



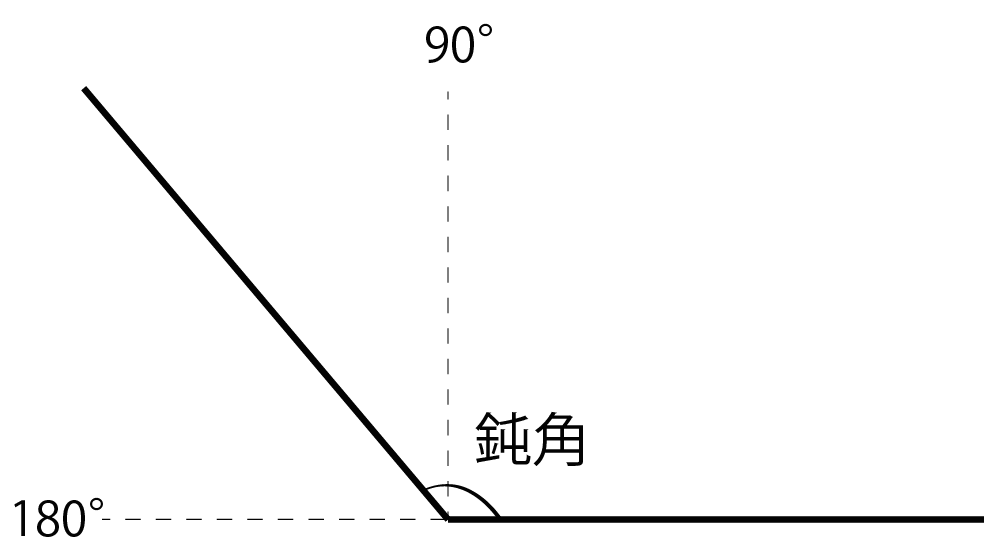
中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく
(鋭角 に対する)三角比の基本関係式 上の直角三角形において, (a とc の関係) a = csin , c = acsc (= a sin ) (b とc の関係) b = ccos , c = bsec (= b cos ) (a とb の関係) a = btan , b = acot (= c tan ) (1)ただし, ,, などの角の大きさには制限がつく。 (2)一般的に,三角関数の相互関係sin2 cos2 = 1 は鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思いますが 図形問題を解いていく上で知っておくと便利な知識でもあります。 abcにおいて、ab=3㎝、bc=4㎝、cd=6㎝とする と問題に出てきたら イメージ図を書きながら問題を解くと鋭角三角形 (えいかくさんかっけい、 英 acute‐angled triangle )は、 三角形 の一種で、すべての角が 直角 (90 ° =π/2 rad) よりも小さい 図形 である。
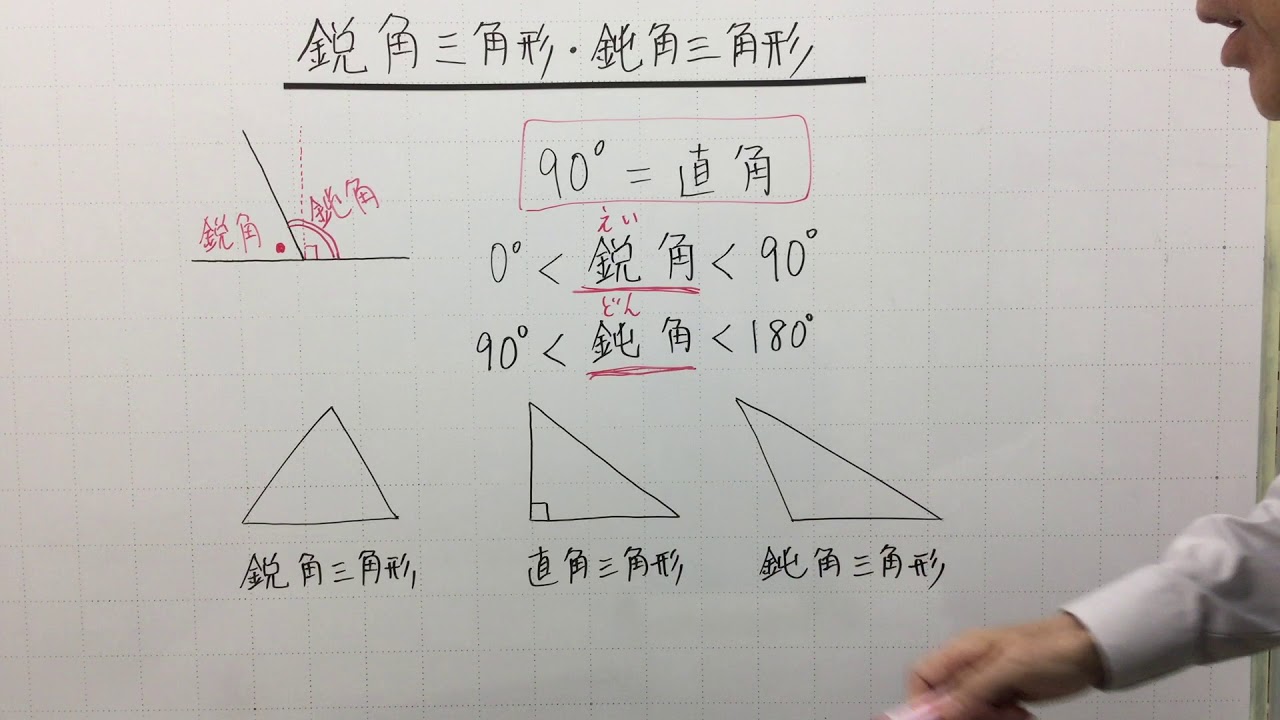
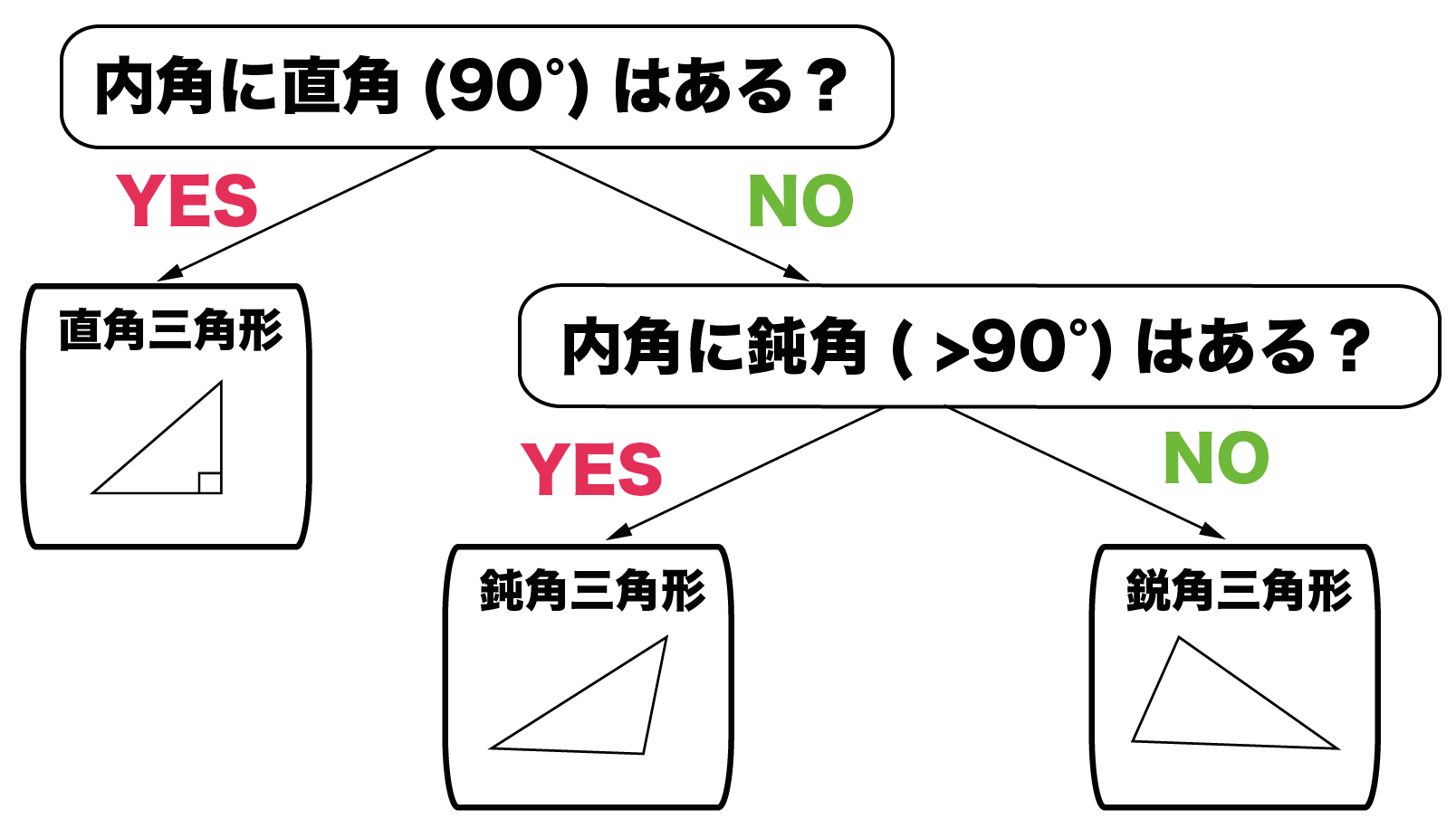
鈍角三角形 (どんかくさんかっけい、 英 obtuse triangle )は、 三角形 の一種で、3つの角のうち、最大角または長辺に対する角が 直角 (90 ° = π /2 rad) よりも大きい 図形 である。そして,三角形はその内角の大きさによって, 鋭角三角形 :3つの内角がすべて鋭角である三角形 直角三角形 :1つの内角が直角である三角形 鈍角三角形 :1つの内角が鈍角である三角形 のように分類されます。 このとき,次の表のように,鋭角三角形鋭角(えいかく)の「鋭」は「するどい」とも読みます。 鋭角三角形 とは、1番大きい角度が「するどい」( 90 ∘ より小さい)三角形のことです。
また、鋭角三角形の辺の個数kを、途中の頂点で別れている者として(えー、つまり無理矢理四角形と見て)数えると 2k=3mab3 ab=m1を代入して 2k=4m2。 ところが、線分の総数は、各頂点に注目して鈍角三角形の三頂点はそれぞれの頂点から3,2,2本以上の線分が伸びていて 内部・周上の分点から直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った /三角形が鋭角三角形になる確率 平成21 年2 月23 日 ランダムな三角形についての考え方を現代確率論の立場から説明するのがこの ノートの目的である。以下の例はいずれもネット上で提案されている。このノー トの内容はこれらを統一的な視点から整理したものと考えていただきたい。 1 確率




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく



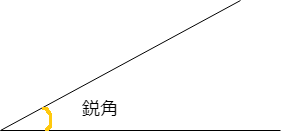
鋭角とは 1分でわかる意味 定義と求め方 0度 範囲 鈍角との違い
三角形は内角の大きさによって, 3 3 種類に分けられます. すべての内角が 90° 90 ° 未満のとき, 鋭角三角形 と言います. 一つの内角がちょうど 90° 90 ° のとき, 直角三角形 と言います. 一つの内角が 90° 90 ° より大きいとき, 鈍角三角形 と言います.鋭角三角形 3つの内角がすべて鋭角である三角形を,鋭角三角形という。 a b c fÿ fÿ f ÿ 0 より大きく90 より小さい角を,鋭角という。 例えば,正 三角形は3 つの角がどれも60 だから,鋭角三角形であ鋭角三角形の特徴とタイプ の 三角形三角形 3つの内角が鋭角の角です。 つまり、これらの各角度の測定値は90度未満です。




A30 Abc Lihat Cara Penyelesaian Di Qanda




直角三角形の合同条件 算数 数学が好きになりmath
三角形の三つの頂垂線(場合によってはその延長線)は、三角形の垂心 h と呼ばれる一点において交わる。 。垂心が三角形の内部にあるための必要十分条件はその三角形が鋭角三角形(すべての角が直角以上になることがない三角形)となることである。 一つの角が直角ならば、垂心はその 16年 東大文系数学 第1問(三角形の成立条件、鋭角三角形の条件、領域図示) 4問のうち、一番得点が取りづらい問題この年の東大入試は僕が実際に受けたものです。そして実際に受けたとき、冊子をめくった瞬間、この問題だけ点数が取り辛いと一瞬で分かります。 z を複素数とする。複素数平面上の3点 A ( 1 ) , B ( z ) , C ( z2 ) が鋭角三角形をなすような z の範囲を求め、図示せよ。16 東京大・理イズミの解答への道 複素数平面で問題は与えられているが、三角関数



第 6 回大会 08 問題一覧




数i 必要十分条件の判別 鋭角三角形など Youtube
Acute‐angled triangle)は、三角形の一種で、すべての角が直角 (90°=π/2 rad) よりも小さい図形 辞書 「鋭角三角形」で始まる言葉 辞書すべて gooIDでログインするとブックマーク機能がご利用いただけます。保存しておきたい言葉を0件直角三角形の左端の角度が45度(直角二等辺三角形)の時の比率は次のようになります。 1対1対√2(いったいいったいルートに) (底辺a=1、対辺b=1、斜辺c=√2) 1対2対√3と1対1対√2を呪文のように何回でも比率を唱えていれば覚えられますので、しっかり頭の中に叩き込みましょう。 また オイラー線 鋭角三角形 ABC ABC について,その外心と垂心をそれぞれ O O と H H とおく。 辺 BC BC の中点を M M として,中線 AM AM と線分 OH OH の交点が ABC ABC の重心であることを証明しよう。 このことが証明されると,三角形の垂心,重心,外心は一直線上に



1




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
三角形分割 の結果として,与えられた矩形を覆う 1 つの大きな三角形が作 成されることに注意してください. opencvjp Note that the triangulation is a singl e鋭角、鋭角三角形の意味は下記が参考になります。 鋭角とは?1分でわかる意味、定義と求め方、0度、範囲、鈍角との違い 鋭角三角形とは?1分でわかる意味、条件、直角三角形、鈍角三角形との違い 100円から読める!ネット不要!動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




動画 三角形の分類 Youtube



コマネチ大学数学科115講 頂点 ガスコン研究所
鋭角三角形 (えいかくさんかっけい、 英 acute‐angled triangle )は、 三角形 の一種で、すべての角が 直角 (90 ° =π/2 rad) よりも小さい 図形 である。鋭角三角形 出典 フリー多機能辞典『ウィクショナリー日本語版(Wiktionary)』 ナビゲーションに移動 検索に移動 鋭角三角形 目次 1 日本語 11 名詞 111 翻訳; 直角三角形で、1つの鋭角が決まれば、もう1つの鋭角の大きさも決まります。すなわち、斜辺とその両端の角が決まるので三角形は1通りに決まります。よって、この条件を満たせば、2つの直角三角形は合同となります。 (ⅱ) 斜辺と他の1辺がそれぞれ等しい。 このことから、「斜辺と他の1



中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく



2
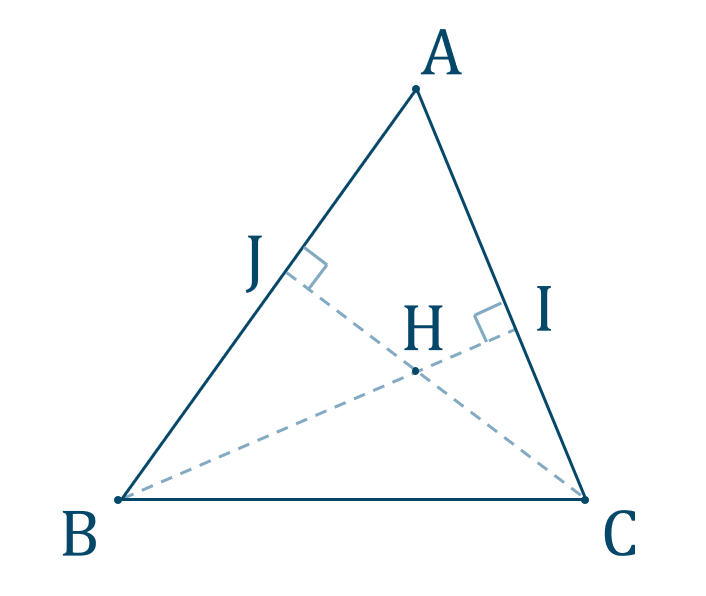
鋭角三角形ABCの各辺BC,CA,AB上にそれぞれD,E,Fをとる.このとき, DE+EF+FDを最小にするD,E.Fは各頂点から対辺に下ろした足である. この章の目的はこの定理を証明することです. さて,証明に入る前に,証明で用いる性質を確認しましょう.この性質はこれからの議論の土台となり2.鋭角の三角比 ここでは,前の章で説明した三角比の定義だけでは,まだ理解できないと思いますので,いろいろな三角形を用いて三角比の定義の理解を深めていくことにしましょう。そこで,もう一度,三角比の定義のおさらいをしてきます。 定義1 (鋭角の三角比) ABC において,三角比を次問題2 鋭角三角形 の内部に点 をとり,線分の長さ和 が最小になるように したい。点 の位置をどこにとればよいか。 ( ヒント 正三角形 , をつくって考える。) 問題3 鋭角三角形 の頂点を除く辺 , , 上にそれぞれ点 , , をとり,線分 の長さ和
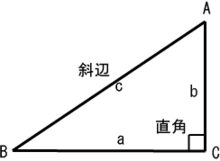



直角三角形 Wikipedia



Kadai78
日本語 名詞 鋭角 三角形 (えいかくさんかくけい, えいかくさんかっけい) 三角形のうち、3つが内角の全て 90度 未満三角形の形状判定 (鋭角・直角・鈍角) の対応動作環境 ソフト名: 三角形の形状判定 (鋭角・直角・鈍角) 動作OS: Windows 10/8/7/Vista/XP 機種: IBMPC x64 種類: シェアウェア :100円鋭角三角形 (えいかくさんかっけい、 英 acute‐angled triangle )は、 三角形 の一種で、すべての角が 直角 (90 ° =π/2 rad) よりも小さい 図形 である。




三角形の成立条件と鋭角 直角 鈍角三角形の判定 数学の偏差値を上げて合格を目指す




Barsquare Ac8bc7 Abc Descubre Como Resolverlo En Qanda
三角形の五心⑤ 三角形の傍心とその存在証明 重心・内心・外心・垂心のうち2つが一致する三角形は正三角形であることの証明 三角形の重心・外心・垂心の位置関係(オイラー線)の幾何的証明
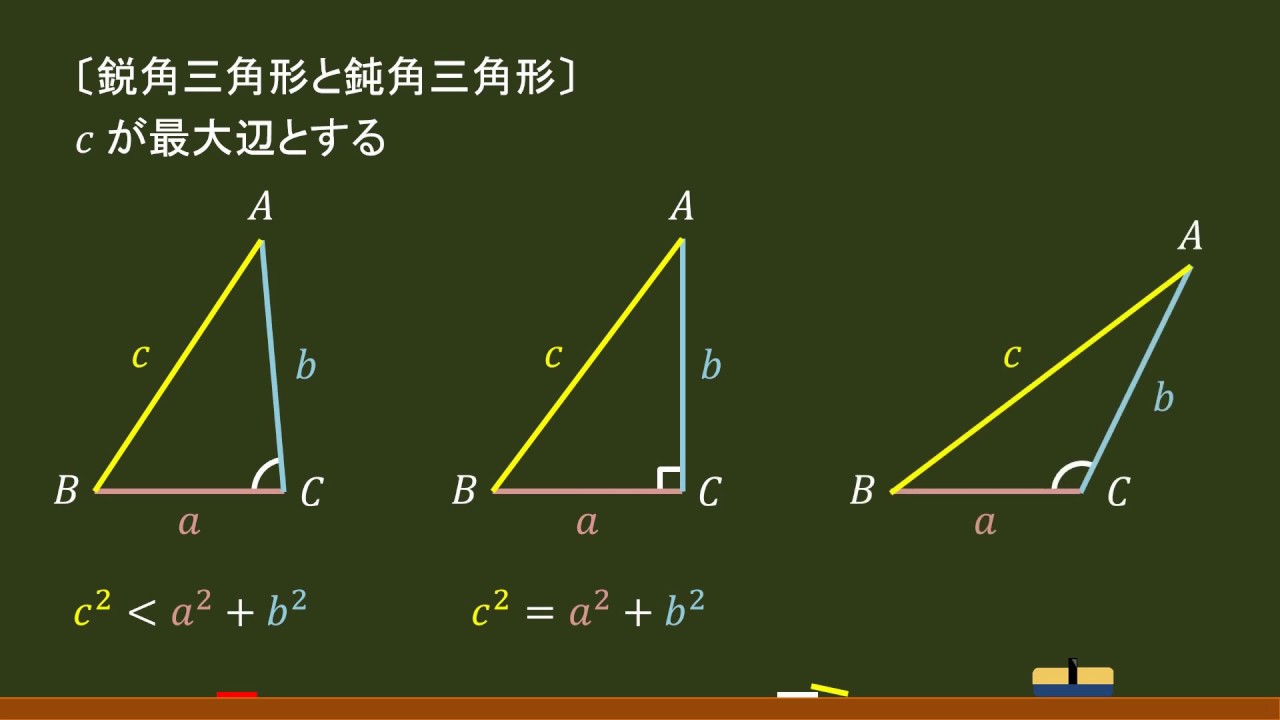



高校数a 図形 鋭角三角形 鈍角三角形の判別方法 オンライン無料塾 ターンナップ Youtube



中学3年数学平面図形鋭角三角形abcの頂点b Cから辺ac Yahoo 知恵袋




中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく



Triangles
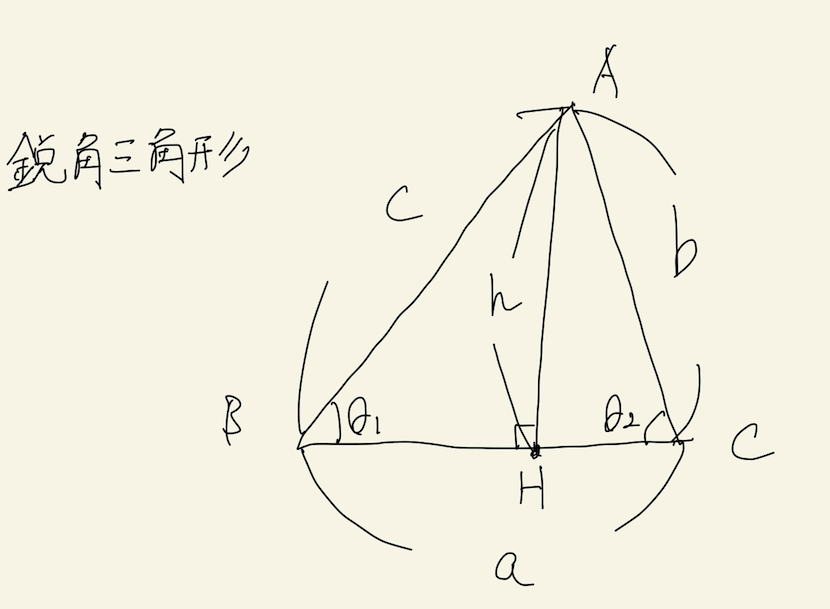



任意の三角形の垂線とその足による内分点の性質 物理u数学の友 質問 悩みに回答します
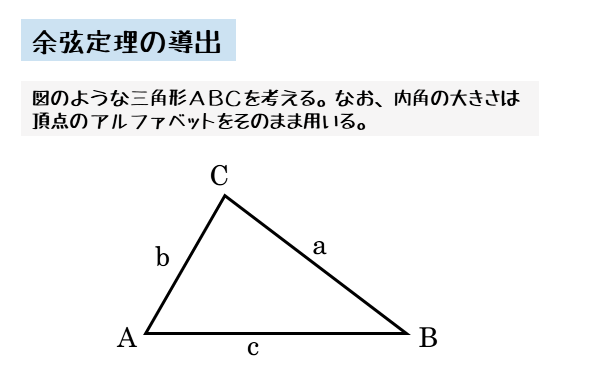



図形と計量 余弦定理について 日々是鍛錬 ひびこれたんれん



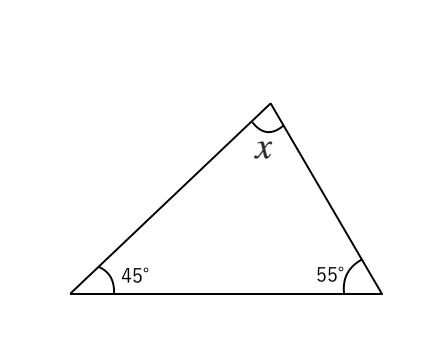
無料 中2数学 基本解説 問題プリント 222 図形2 三角形の角




中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau



全て の 角 が 90 の 三角形
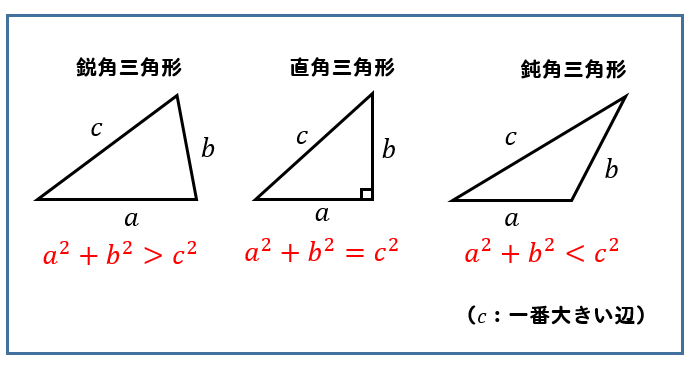



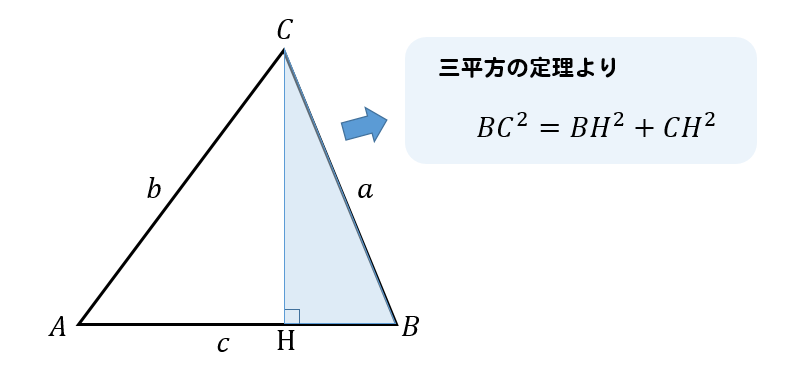
鋭角 鈍角三角形 三平方の定理を使って見分ける方法を解説 数スタ




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月




高校数学a 三角形の重心 外心 垂心の位置関係 オイラー線 の幾何的証明 受験の月




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく




数学 中2 50 鋭角三角形と鈍角三角形 Youtube



Abc 3 Abc Lihat Cara Penyelesaian Di Qanda




京都大学 理系 19年度 第3問 解説 ページ 2 なかけんの数学ノート




三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




なぜこれで三角形が鋭角三角形であることを示せるんですか Clear




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強




鈍角三角形 鋭角三角形の見分け方 高校数学 Youtube




この65番の問題がわかりません Clear




高校数学 三角形の鋭角 直角 鈍角条件 三角形の成立条件3パターン 受験の月




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく




1 の 三角形abcが鋭角三角形になる時のxの範囲はどうやって求めるんですか Clear



中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強



中2数学 鋭角三角形 鈍角三角形 0991 Youtube




高校数学を初めから丁寧にvol 077 数学i 三角関数 鋭角三角形 鈍角三角形の判定 Youtube



余弦定理の証明 簡単にわかりやすく考えてみよう 数スタ



数学ia 三角形の角の大きさと辺の長さの関係 大学入試数学の考え方と解法



2




無料 中2数学 基本問題 問題プリント 223 図形3 多角形の角



鈍角 三角形 条件 鈍角三角形の合同について



1




余弦定理 Wikiwand




鋭角三角形 Wikipedia




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強



数学a 三角形の垂心の性質の使い方とコツ 教科書より詳しい高校数学



1




鋭角三角形 直角三角形 鈍角三角形かを調べる方法 数学i By ふぇるまー マナペディア




解説です Abcが鋭角三角形から角aがなぜ90 未満とわかるのですか Clear




鋭角三角形と鈍角三角形の意味と見分け方 具体例で学ぶ数学



この数学の問題教えてください 三角形abcにおいて 3辺の長さが次 Yahoo 知恵袋




岐阜薬科大学 薬学部 11年問題5 Suugaku Jp




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強




直角三角形の合同条件とその証明 数学fun



Renew E School E Tokushima Or Jp Tokushima Jh Joto Wysiwyg File Download 1 243



直角 鋭角 鈍角三角形の判定法 思考力を鍛える数学




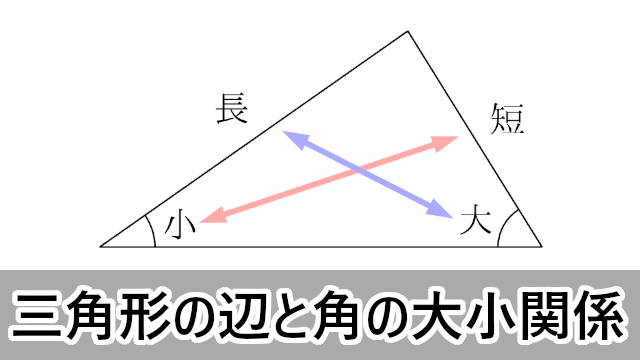
高校数学 三角形の辺と角の関係 映像授業のtry It トライイット




図形と計量 三角形の面積について 日々是鍛錬 ひびこれたんれん
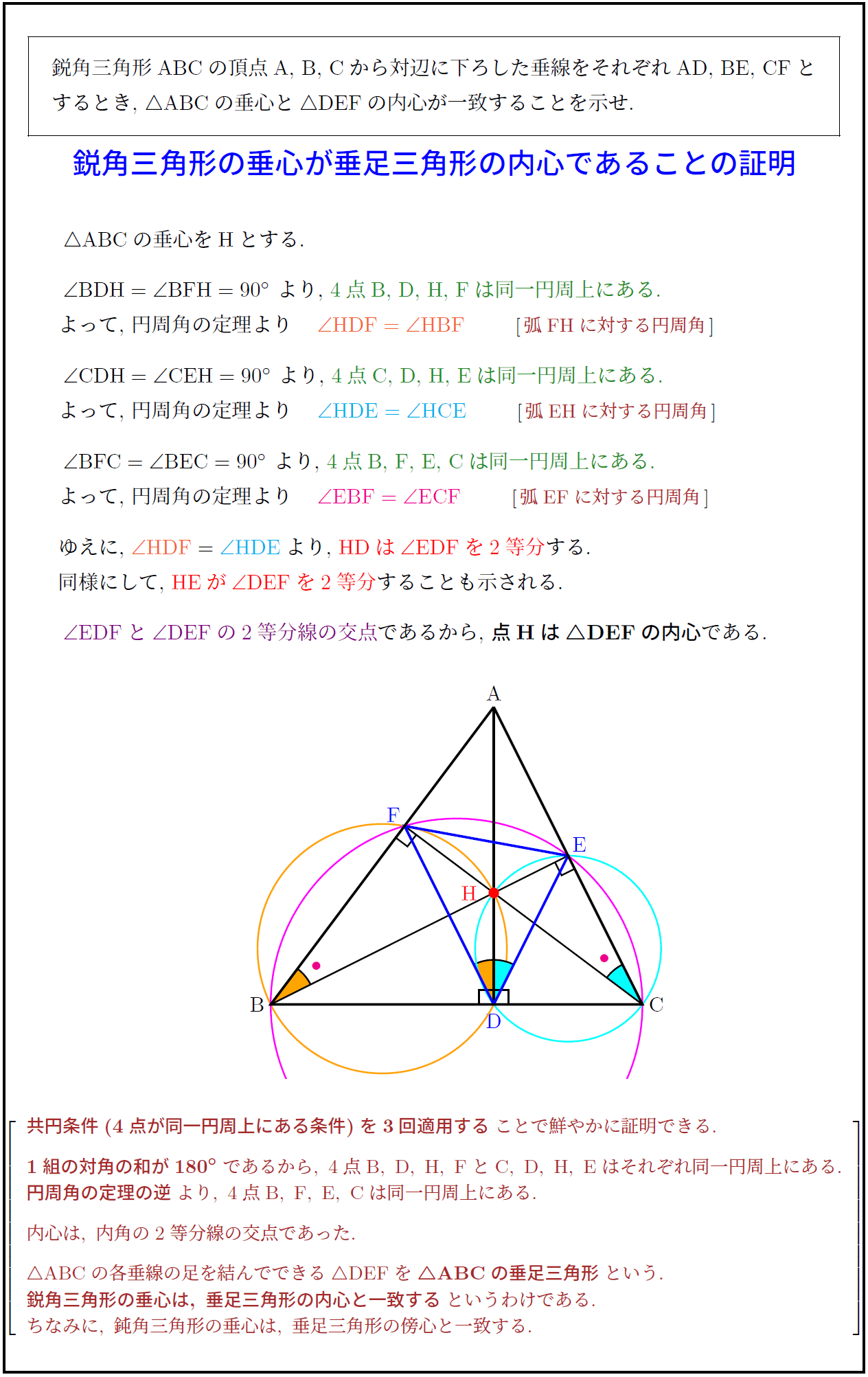



高校数学a 鋭角三角形の垂心が垂足三角形の内心であることの証明 受験の月




黄金三角形による18 シリーズの三角比 おいしい数学



鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく




鋭角三角形



鋭角三角形とは 1分でわかる意味 条件 直角三角形 鈍角三角形との違い




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく



外接円 外心について



鈍角三角形の分割




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強



鋭角三角形 数学入試問題




正弦定理とその証明を勉強しよう スタディクラブ情報局



鋭角三角形の周




中学2年の数学 動画 鋭角三角形と鈍角三角形の問題 19ch



三角形とは コトバンク




鈍角三角形 鋭角三角形 直角三角形の違いを詳しく教えてください お願いします Clear




鈍角三角形 直角 鋭角 鈍角三角形の判定法 思考力を鍛える數學翻譯此網頁 Patry Kdas




Ce E D Descubre Como Resolverlo En Qanda



鈍角三角形の分割



Iidrill Com Wp Content Uploads 19 11 E4 B8 96 E7 95 8c E4 B8 80 8f 81 8b 8a 81 99 81 84 E4 B8 Ad Ef 92 E6 95 B0 E5 Ad A6 Ef 94 E7 Ab A0k 11 Pdf



三角形の計算 もう一度やり直しの算数 数学




鋭角三角形 直角三角形 鈍角三角形って何が違うんですか 教えてください Clear




2016年 東大文系数学 第1問 三角形の成立条件 鋭角三角形の条件 領域図示 オンライン受講 東大に 完全 特化 東大合格 敬天塾



鋭角三角形の確率




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強




鋭角三角形と鈍三角形正三角形幾何学 三角形 鋭角と鈍角の三角形 角度 角度鈍角 Png Pngwing




直角三角形の辺の長さ 合同条件 面積について アタリマエ



48s96ub7b0z5f Net Sankakuhi Seiritsujouken Katachi



鋭角三角形とは 1分でわかる意味 条件 直角三角形 鈍角三角形との違い



2016年 東大数学 理系第4問 三角形をなす条件 鋭角三角形の条件 複素数平面 オンライン受講 東大に 完全 特化 東大合格 敬天塾




1 の 三角形abcが鋭角三角形になる時のxの範囲はどうやって求めるんですか Clear




中2 数学 中2 43 鋭角三角形 鈍角三角形 Youtube



中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強




14 号 図形板セット Astamuse



図形の調べ方 三角形についてまるわかり 苦手な数学を簡単に




Kistenkasten723 啓林館の教科書は 小5面積の章は 1 三角形の面積の節 直角三角形 鋭角三角形 2 平行四辺形の面積の節 3 面積の公式を使って 鈍角三角形 などに分かれていています



0 件のコメント:
コメントを投稿